君たちの弱点はどうも「単位の計算」と「文章題」のようだね。 ちょっとだけ練習してみようか？

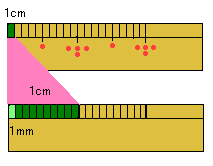
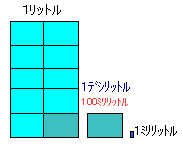
まずは「基本」。 　「1mm」と「1cm」のかんけいおぼえているかな？ 左の図は，教科書でもよく見ますよね。 　まあ，「1cmをマッチ箱」「1mmをマッチ」 にたとえて言うなら… 『マッチ箱にマッチが１０本入っている』 のと同じかな？ 　こんなふうにかんがえると，２学期にならう「m」は… 『大きな箱にマッチ箱が１００個入っている』 という感じになるけどわかる？ この場合『大きな箱』というのが「ｍ」だよ。 　「水のかさ」の場合， 「１ﾃﾞｼﾘｯﾄﾙ」と「１ﾘｯﾄﾙ」では，長さのかんけいと ちょっとちがっているけど， かんがえ方は同じだよ。 　「長さの計算」や「かさの計算」の場合，「ｃｍ」は「ｃｍ」 どうしで計算するように，同じ単位のなかまどうしで計算 していきます。 　しかし…なかまがいない時は，どうでしょう？ 足し算の時は， 大きい単位のものからならべて書けばいいけど， 引き算の場合は… そう！なかまをつくればいいのです。 　『１ｃｍ−1mm』のような計算は 『10mm−1mm』としてやると 計算できますね(*^,^*) ☆ ただし，これだけは知っておこう！ 答えで 「1cm10mm」いうふうになる場合がありますね。 これは×になります。 なんで？ かんがえてごらん(*^,^*)

今度は文章題ね…そこで 「計算問題はできるのに…」 こんなお友達がとても多いなあ。 「計算」というのは「文章題」に書かれている内容のように， 私たちの身の回りに関わる問題を解くために使われる「１つの方法」なんだから 計算でいくら１００点とっても正直言って役に立つのはテストだけ！ なんだかさみしいぞお〜 ☆ まあ，ここで問題を出しても良いけど，まずは 『見直し』だね！ そして… 『物を作る遊び』『手伝い』など，いろいろ経験することだな。 例えば… 『１円玉の幅はどのくらい？』 とか， 『２年生が１０分かけて歩くと，どのくらいすすむ？』 とか， 『自転車に１時間のってすすむ距離は？』 とか， 『両手ですくえる水の量は？』 なんて質問されたとき，なんてこたえる？ 「習ってませ〜ん」 じゃあ，あまりにもさみしいねえ。 ☆ そこで宿題 ☆ 身の回りのものを見たりさわったりしたときに，（買い物も） 「これはどれくらいかな？」 と予想して，確かめてみること！ どれだけ正確に予想できるでしょうねえ(*^,^*) ☆ これって，けっこう役に立つ勉強なんだよ！